Load Packages

library(tidyverse)
library(carData)
library(knitr)
library(fivethirtyeight)
library(broom)

GSS Vocab Data (Categorical)

For the purpose of today’s chat, we’ll look at the data collected from the US General Soceity Survey from the National Opinion Research Centre of the University of Chicago.

GSSvocab %>% 
  View()
  # Use the Viewer, summary, glimpse

Based on the data, we can see there are entries for the year, the gender, whether born in US, the age group, the education group, vocab, age, and education.

Let’s begin to explore and summarize the data using the count function.

GSSvocab %>% 
  count(educGroup)

## # A tibble: 6 x 2
##   educGroup     n
##   <fct>     <int>
## 1 <12 yrs    5924
## 2 12 yrs     8612
## 3 13-15 yrs  7182
## 4 16 yrs     3914
## 5 >16 yrs    3154
## 6 <NA>         81

Maybe, based on these counts, I want to see whether there is a relationship between two categorical variables. Let’s take a look at whether being native born seems to have some association with one’s education group?

GSSvocab %>% 
  group_by(nativeBorn, educGroup) %>% 
  summarise(n = n()) # n() counts the number of observations of each factor

## Warning: Factor `nativeBorn` contains implicit NA, consider using
## `forcats::fct_explicit_na`

## Warning: Factor `educGroup` contains implicit NA, consider using
## `forcats::fct_explicit_na`

## Warning: Factor `nativeBorn` contains implicit NA, consider using
## `forcats::fct_explicit_na`

## # A tibble: 18 x 3
## # Groups:   nativeBorn [3]
##    nativeBorn educGroup     n
##    <fct>      <fct>     <int>
##  1 no         <12 yrs     690
##  2 no         12 yrs      520
##  3 no         13-15 yrs   586
##  4 no         16 yrs      369
##  5 no         >16 yrs     381
##  6 no         <NA>         10
##  7 yes        <12 yrs    5215
##  8 yes        12 yrs     8067
##  9 yes        13-15 yrs  6583
## 10 yes        16 yrs     3538
## 11 yes        >16 yrs    2765
## 12 yes        <NA>         56
## 13 <NA>       <12 yrs      19
## 14 <NA>       12 yrs       25
## 15 <NA>       13-15 yrs    13
## 16 <NA>       16 yrs        7
## 17 <NA>       >16 yrs       8
## 18 <NA>       <NA>         15

It looks like we’re dealing with missing data, so let’s filter the data to only include data that is included. R has many convenient commands that allows us to remove the NA values.

GSSvocab %>% 
  drop_na() %>% 
  group_by(nativeBorn, educGroup) %>% 
  summarise(n = n())

## # A tibble: 10 x 3
## # Groups:   nativeBorn [2]
##    nativeBorn educGroup     n
##    <fct>      <fct>     <int>
##  1 no         <12 yrs     597
##  2 no         12 yrs      475
##  3 no         13-15 yrs   548
##  4 no         16 yrs      353
##  5 no         >16 yrs     369
##  6 yes        <12 yrs    4667
##  7 yes        12 yrs     7784
##  8 yes        13-15 yrs  6394
##  9 yes        16 yrs     3461
## 10 yes        >16 yrs    2712

Let’s visualize this in a plot. Let’s use a bar plot to see the relationship between the distribution of education levels across these two groups. From this data, we have a decent understanding of how to look at the relationships between categorical variables. Now, we’re going to take a dive into the relationship between different types of variables related to the wages that recent college graduates earn.

GSSvocab %>% 
  drop_na() %>% 
  ggplot(aes(x = nativeBorn, fill = educGroup))+
  geom_bar(position = "fill") #change to fill after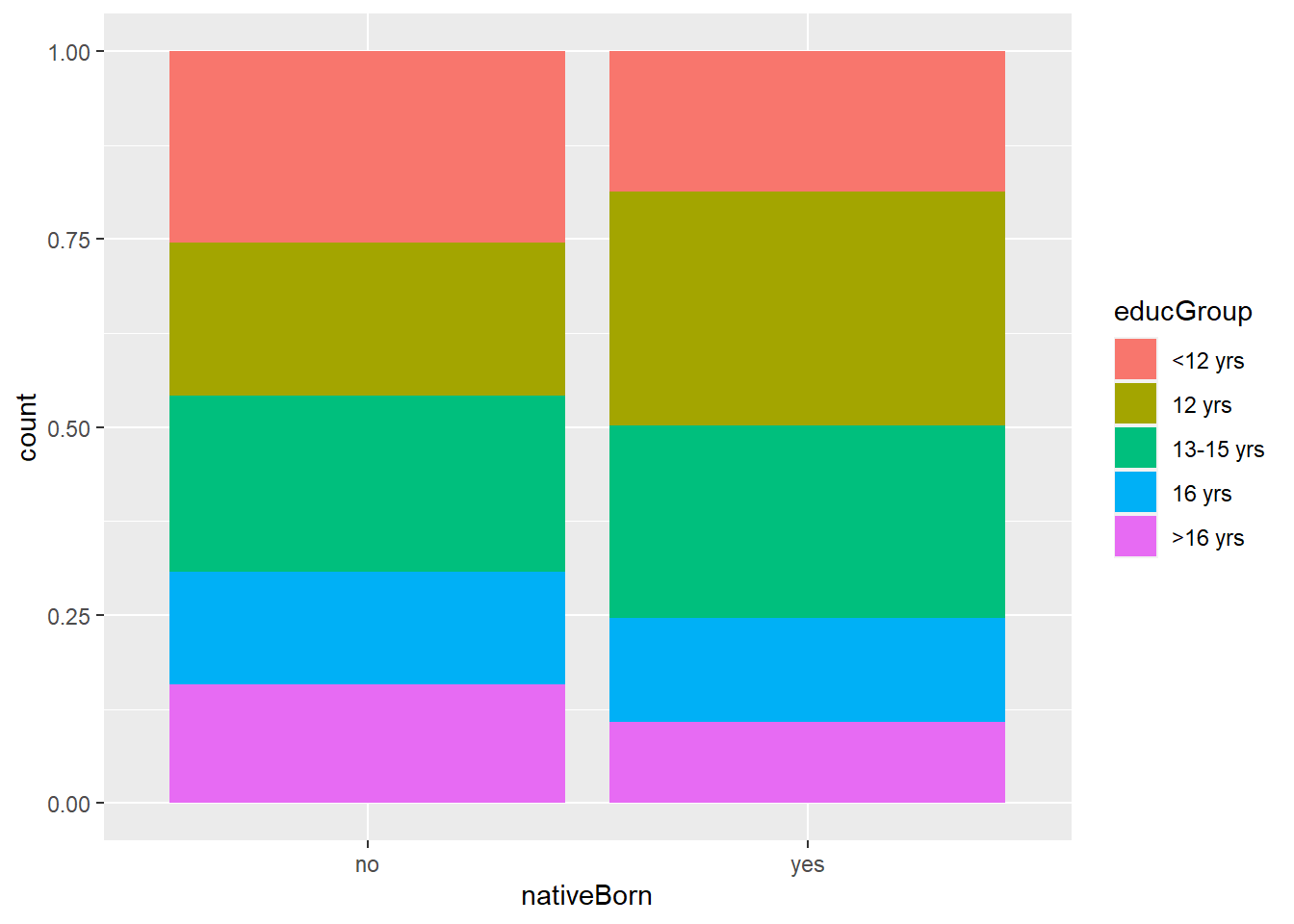

FiveThiryEight Data (Numerical)

One perk of using R is that many organizations offer open data that are stored in R. We can use the fivethirtyeight package to use investigate some of the data that the website fivethirtyeight.com uses for its stories. In fact, most of the journalists who are using data to report their stories offer open access to their repositories and code. For instance, FiveThirtyEight uses this website for its repositiory. Much of the data is also stored on a GitHub repository for others to replicate analysis.

Let’s look at a dataset of a sample of recent college graduates and is used to produce this article. In order to access the data, let’s call it using R. Then, we can inspect the data, and hopefully come up with a question to answer.

college_recent_grads # %>% 
 # View()

Let’s take a quick look at the basic metrics for the median variable. The median wage of the college graduates who were sampled. There are 173 majors included here. First, a histogram. From this, we can describe its shape, centre, and spread. I’ve added a colour outline to make the bins more obvious.

college_recent_grads %>% 
  ggplot(aes(x = median))+
  geom_histogram(colour = "white")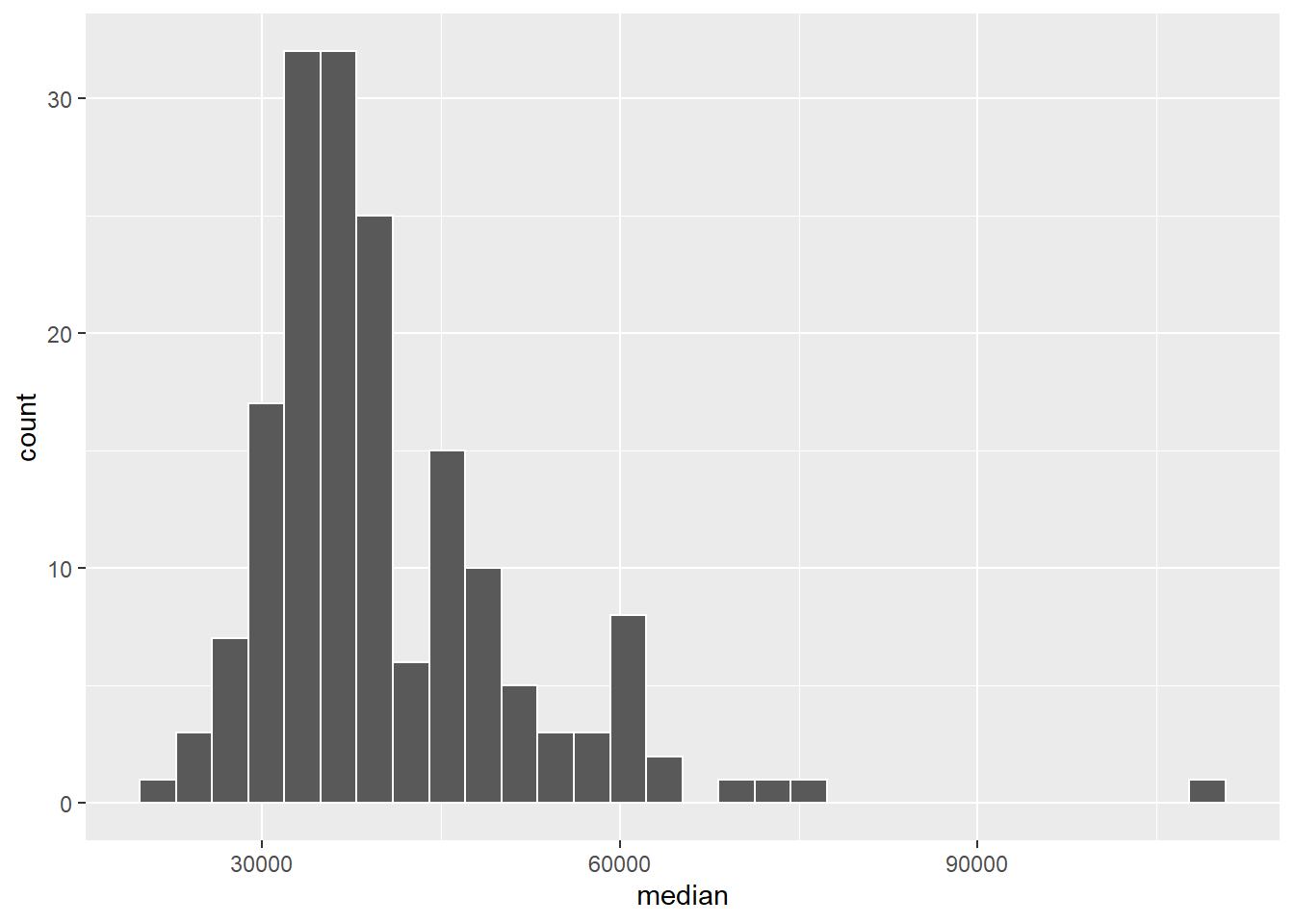

Shape: There are some obvious outliers to the right, and it is skewed-right.

Centre: The median appears to be around $35,000.

Spread: The spread is high relative to the median.

Now, let’s find some actual values for these using summary statistics. You’ll find this code is very intutive in regard to the way we think about computing statistics. We can alse use the summary() function for these.

college_recent_grads %>% 
  summarise(mean = mean(median), 
            med = median(median), #careful naming your variables here
            sd = sd(median), 
            iqr = IQR(median))

## # A tibble: 1 x 4
##     mean   med     sd   iqr
##    <dbl> <dbl>  <dbl> <dbl>
## 1 40151. 36000 11470. 12000

It might be a good idea to investigate some of the outliers and relationship between the high and low median salaries. Let’s see if there’s a pattern with another variable? Let’s look to see if maybe we can see something with the major category variable.

college_recent_grads %>% 
  count(major_category, sort = TRUE)

## # A tibble: 16 x 2
##    major_category                          n
##    <chr>                               <int>
##  1 Engineering                            29
##  2 Education                              16
##  3 Humanities & Liberal Arts              15
##  4 Biology & Life Science                 14
##  5 Business                               13
##  6 Health                                 12
##  7 Computers & Mathematics                11
##  8 Agriculture & Natural Resources        10
##  9 Physical Sciences                      10
## 10 Psychology & Social Work                9
## 11 Social Science                          9
## 12 Arts                                    8
## 13 Industrial Arts & Consumer Services     7
## 14 Law & Public Policy                     5
## 15 Communications & Journalism             4
## 16 Interdisciplinary                       1

It looks like there are 16 categories. Let’s take a quick look at a boxplot for the median salary of each major category. This is a great way to compare distributions.

college_recent_grads %>% 
  ggplot(aes(x = major_category, y = median))+
  geom_boxplot()+
  coord_flip()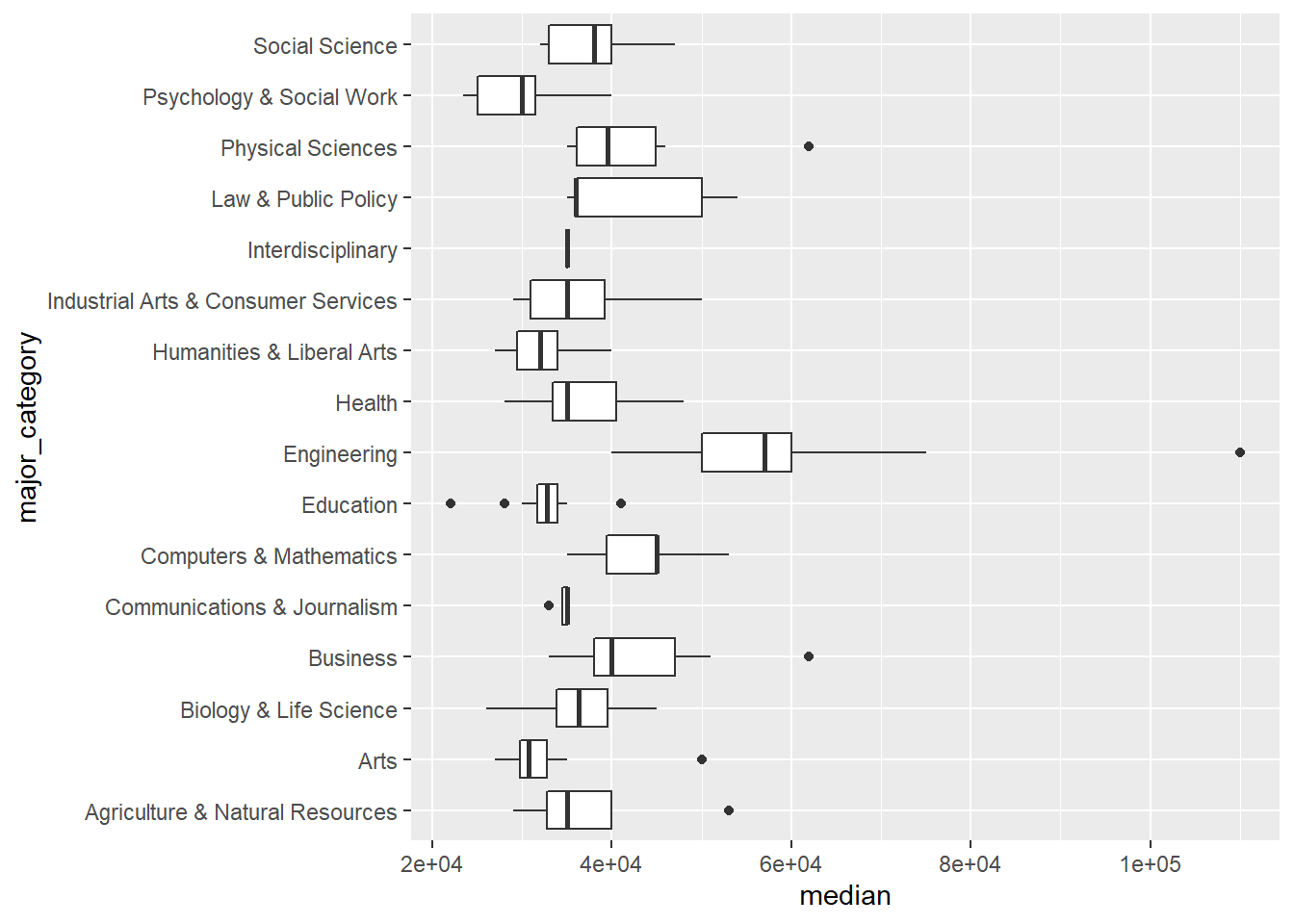

Note that it’s difficult to detect any systematic pattern, so we’ll try and create an ordered list of categories so that we can look for some patterns. If we arrange the categories in order of median salary, we may find some patterns.

college_recent_grads %>% 
  mutate(major_category = fct_reorder(major_category, median)) %>% 
  ggplot(aes(x = major_category, y = median))+
  geom_boxplot()+
  coord_flip()+
  theme_light()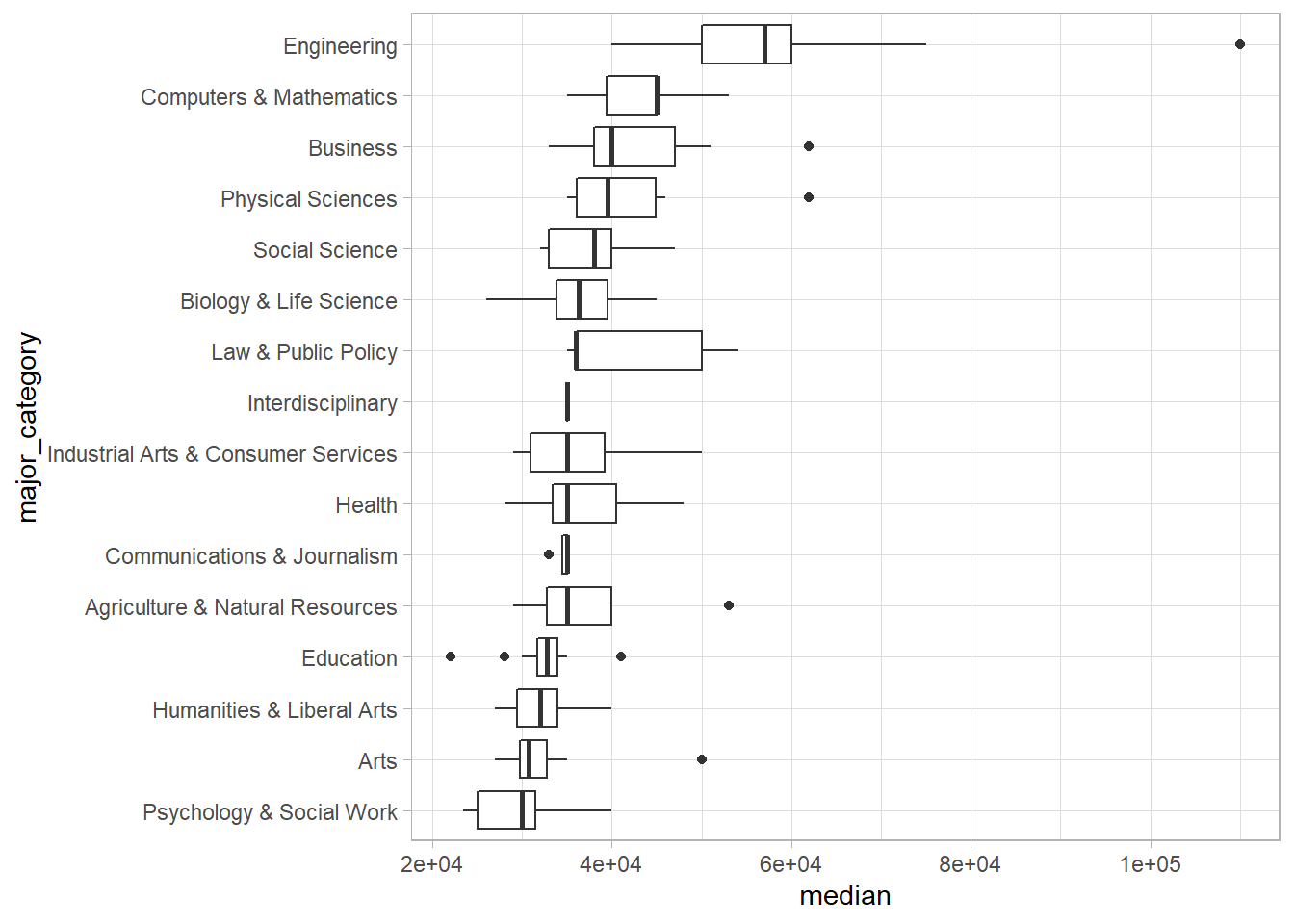

Here’s another way to find the same information, and I made this plot a little more presentable with some titles and colours.

college_recent_grads %>% 
  group_by(major_category) %>% 
  summarise(med = median(median)) %>% 
  ungroup() %>% 
  mutate(major_category = fct_reorder(major_category, med)) %>% 
  ggplot(aes(x = major_category, y = med))+
  geom_col(aes(fill = major_category))+
  coord_flip()+
  theme_light()+
  scale_y_continuous(labels = scales::dollar_format())+
  scale_fill_viridis_d()+
  theme(legend.position = "none")+
  labs(x = "Major Category",
       y = "Median")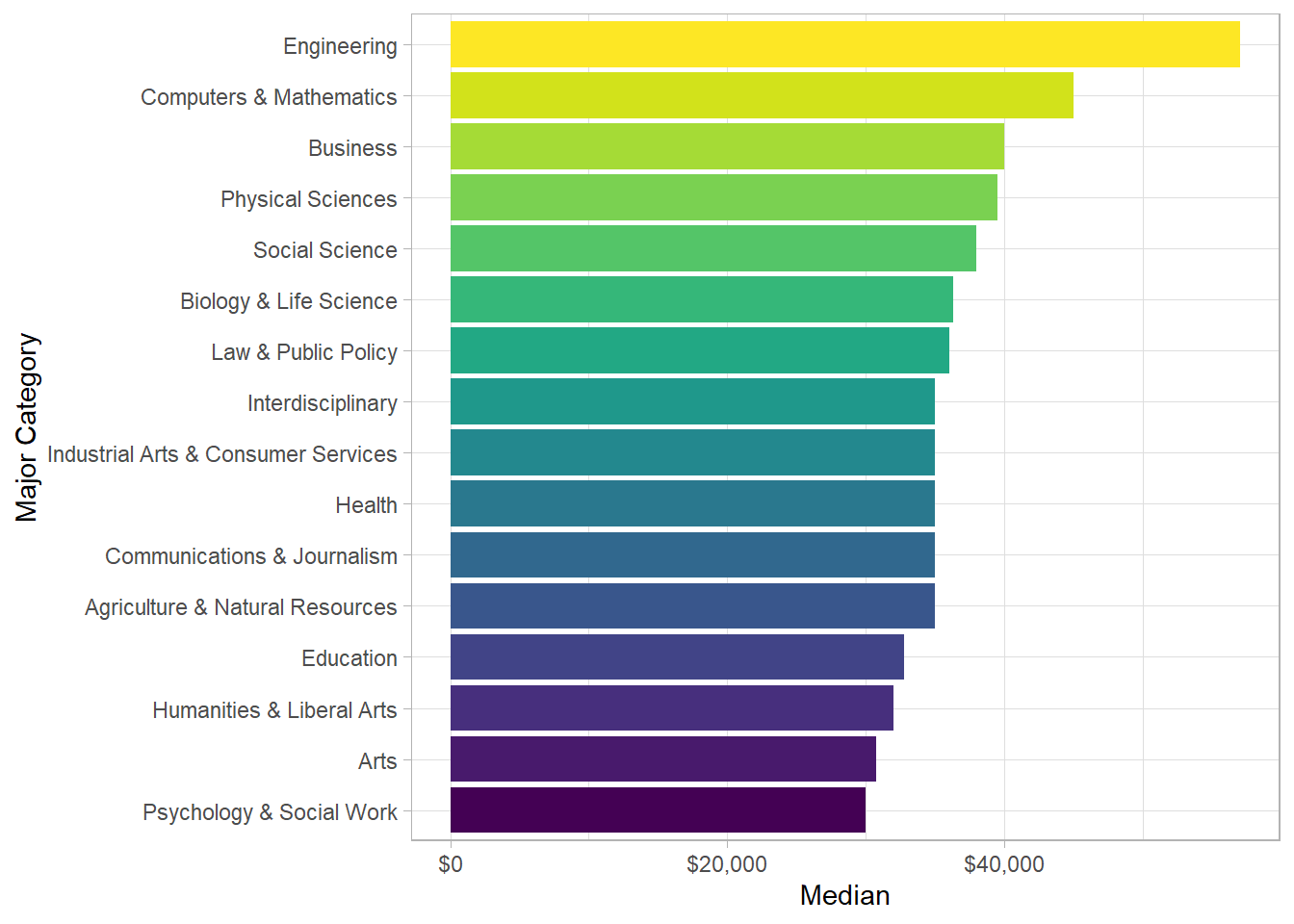

Back to the boxlot. Another issue is that we have 16 categories, and some with only a few majors. Let’s group together interdisciplinary, comms & journ, Law & PP, Ind Arts & CS, and Arts together. That will give us 11 categories and an “other” category. (Let’s work on making this plot a more pleasant in the live session) I’d recommend having your students work with some plots that already exist and modifying them slightly in order to get a handle on the code that changes plots.

college_recent_grads %>% 
  mutate(major_category = fct_lump(major_category, 11)) %>% 
  mutate(major_category = fct_reorder(major_category, median)) %>% 
  ggplot(aes(x = major_category, y = median))+
  geom_boxplot()+
  coord_flip()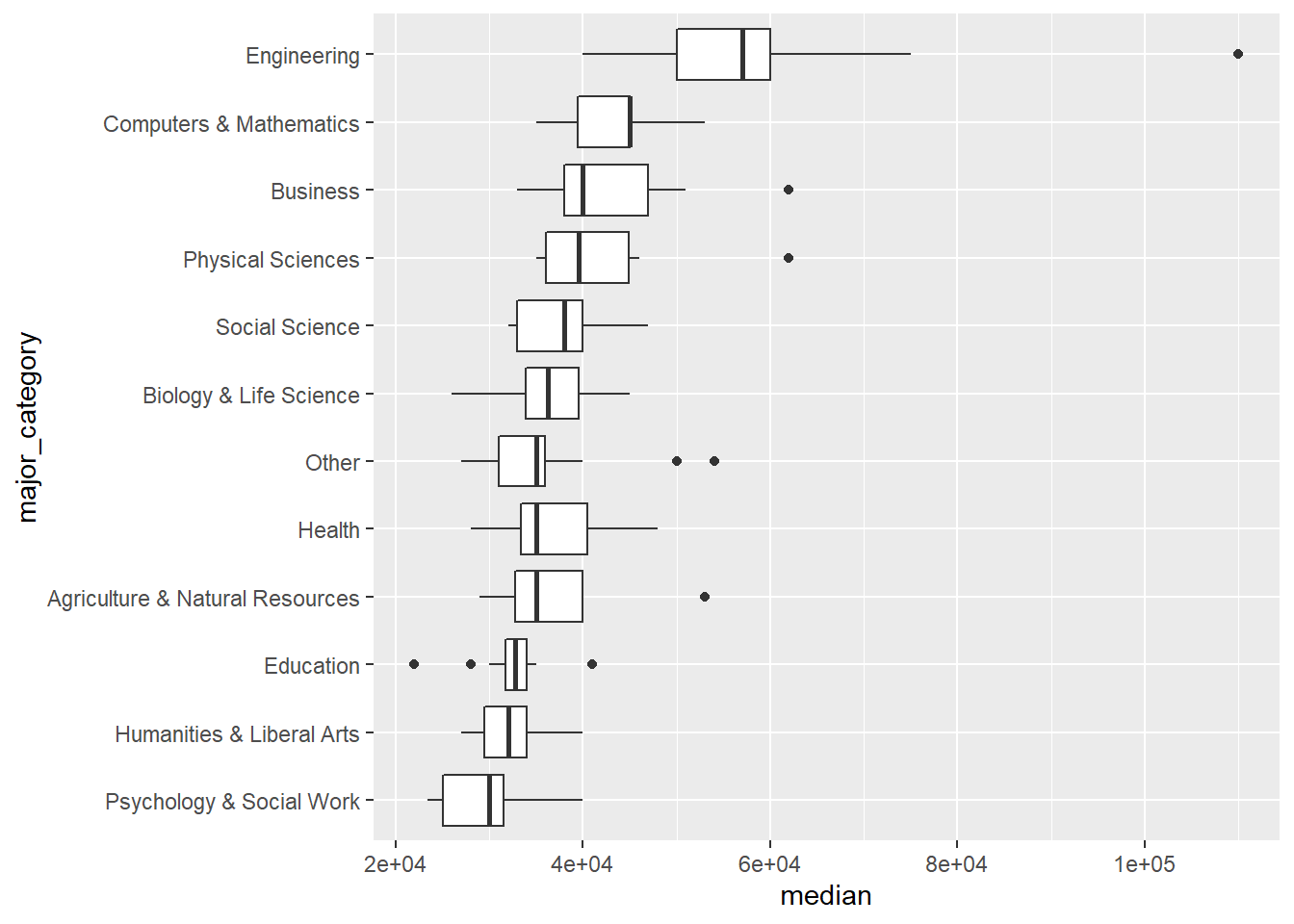

Lastly, let’s look at whether there’s a relationship between the share of women in the major and the median salary in the field. To do this, we can correlation and a plot to get a sense of what this looks like.

college_recent_grads %>%
  #mutate(median = median/1000) %>% 
  #mutate(major_category = fct_reorder(major_category, -median)) %>% 
  select(major_category, sharewomen, median, major) %>% 
  ggplot(aes(x = sharewomen, y = median))+
  geom_point()+ # also add in colour here
  scale_color_viridis_d()+
  theme_light()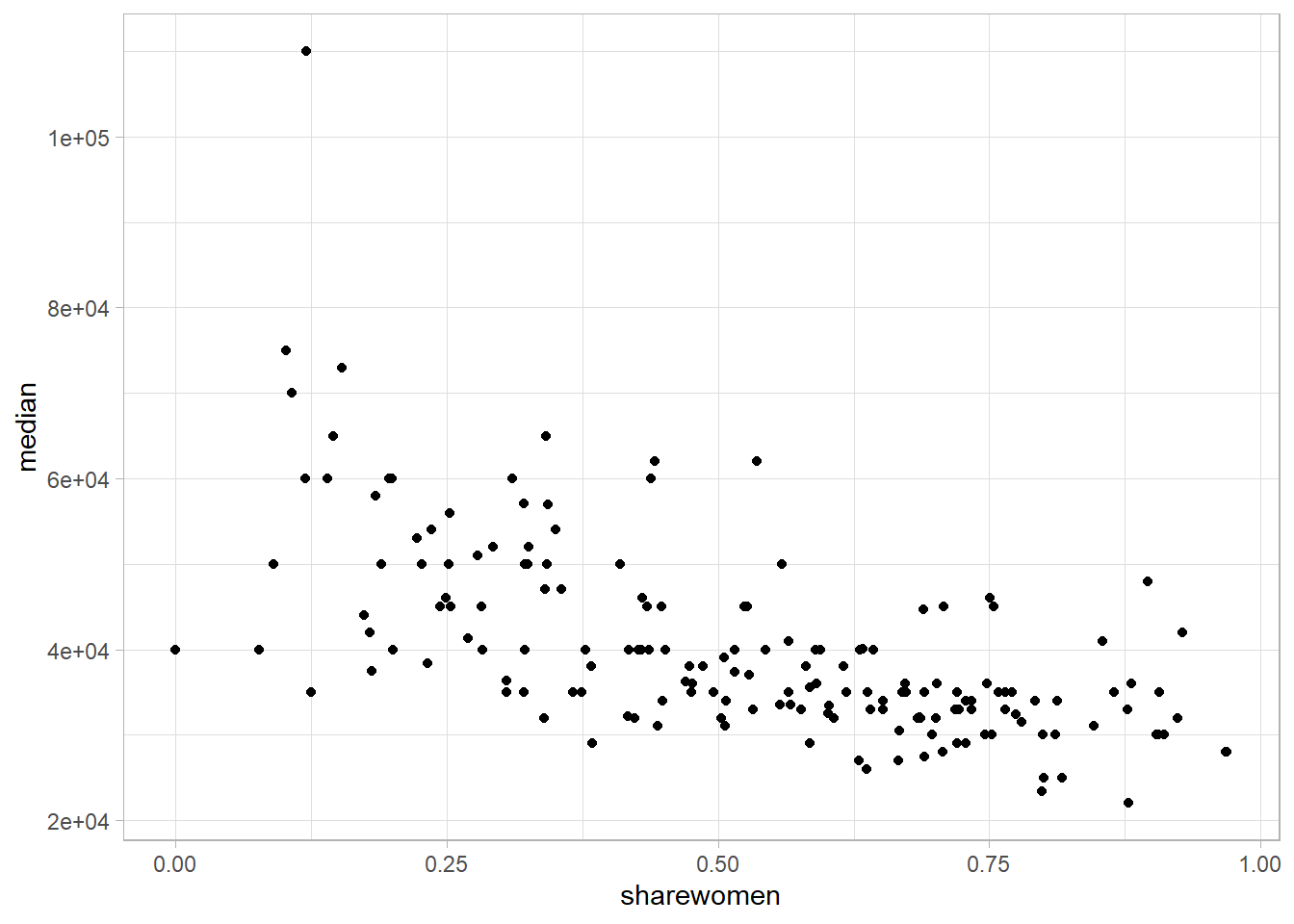

  #geom_smooth(method = "lm") Don't forget to add +

This is a trend that we may want to investigate because it looks like there’s a reasonable association here. The median salary has a moderate, negative and linear relationship with the share of women who are in the field.

Let’s try and fit a model here. Before we fit, we check to see the correlation coefficient between the two variables.

college_recent_grads %>% 
  select(sharewomen, median) %>% 
  cor(use = "complete.obs")

##            sharewomen     median
## sharewomen  1.0000000 -0.6186898
## median     -0.6186898  1.0000000

Now, let’s show a linear model on the data.

college_recent_grads %>% 
  select(sharewomen, median) %>% 
  ggplot(aes(x = sharewomen, y = median))+
  geom_point()+
  geom_smooth(method = "lm")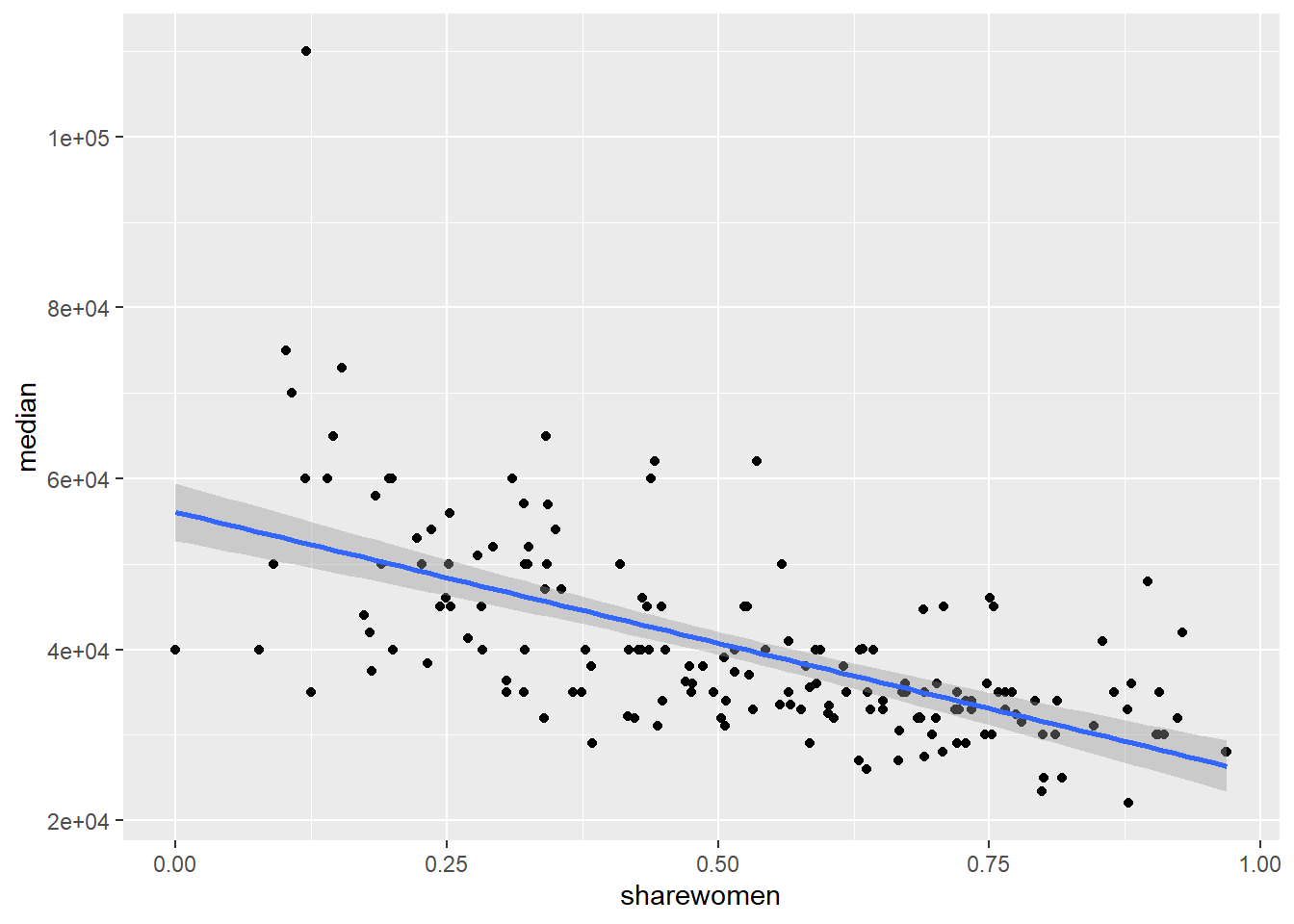

Now, let’s find the model terms and the statistics of the model.

college_recent_grads %>% 
  select(sharewomen, median) %>% 
  lm(median ~ sharewomen, data = .) %>% 
  tidy() %>% 
  kable()

term	estimate	std.error	statistic	p.value
(Intercept)	56093.31	1705.115	32.89708	0
sharewomen	-30669.94	2987.010	-10.26777	0

college_recent_grads %>% 
  select(sharewomen, median) %>% 
  lm(median ~ sharewomen, data = .) %>% 
  glance() %>% 
  kable()

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual
0.382777	0.3791463	9030.918	105.4272	0	2	-1809.698	3625.396	3634.838	13864770781	170